History
Code was written by humans as machine level instructions. As programs got more
complicated the assembly language was created and it was the job of the
assembler to covert assembly language into machine language.
Assemblers eventually were augmented with elaborate "macro expansion" facilities
to permit programmers to define parameterized abbreviations for common sequence
of instructions.
During this time, programming continued to be a machine-centered enterprise:
each different kind of computer had to be programmed in its own assembly
language.
As computers evolved, programmers wanted a language that did not require to be
rewritten on each machine. In the mid-1950s, FORTRAN was created as first
high-level programming language
The late 1960s and early 1970s saw the revolution of "structured-programming"
with the go-to statement introduced, which then gave way to while loops,
switch-case statements, and similar high level concepts.
In 1980s the nested block structure of languages like Algol, Pascal, and Ada,
began to give way to object-oriented programming languages like Smalltalk.
Introduction
Imperative Vs Declarative Programming
Imperative languages describe the steps to solve a problem. Existing
hardware is imperative by nature. Therefore it's easier to map imperative
languages onto machine code. There tends to be a tension between optimality and
readability. It's easier to make subtle mistakes in imperative and hence are
more error-prone (opinion). The program achieve the goal by using
side-effects.
Declarative languages describe the goal of the problem. Some problems are
easier to express declaratively. Due to this nature, programs are often to
reason about and make it easier to parallelize. They often include an evaluation
engine or virtual machine at runtime. Therefore, they are often performance
penalties.
Side Effects
Side effect simple take about the change to a state rather than just processing.
Here is an example to illustrate this point:
int GLOBAL_VAR = 10;
void update_variable() {
GLOBAL_VAR++
}
int updated_variable(int a) {
return a+1;
}
The first function update_variable updates a global variable and hence
changing the state of the program. The second function updated_variable takes
in a variable and just returns the next value. The first has side effects and
the second does not.
Any change to system state is considered a side effect. Examples of this can
include sorting an array in place, update the contents of a variable (a = a +
1), etc.
The Art of Language Design
Functional Languages
Functional languages employ a computational model based on the recursive
definition of functions. They take their inspiration from lambda calculus, a
formal computational model developed by Alonzo Church.
The fundamental concept of functional languages is that they process data by
composing functions. Functions that take in inputs and produce outputs. Such
functions DO NOT modify "state". There isn't a concept of state in
functional programming languages. That is, given the same parameters, the
function always returns the same outputs.
Dataflow Languages
Dataflow languages model computation as the flow of information (tokens) among
primitive functional nodes. They provide an inherently parallel model: nodes are
triggered by the arrival of input tokens, and can operate concurrently.
Logic/Constraint-based Languages
Logic or constraint-based languages are inspired by predicate logic. The model
computation as an attempt to find values that satisfy certain specified
relationships. You provide the language information and then you can query the
language about the data.
von Neumann Languages
von Neumann languages are structured around computation that work by
modification of variables. These languages are based on expressions that have
values that influence subsequent computation via the side effect of
changing the value of memory.
Object-oriented Languages
Object-oriented languages are closely related to the von Neumann languages, but
have more structured and distributed model of both memory and computation. It
creates the construct of objects and methods (function) associated with those
objects.
Scripting Languages
Scripting languages are focused on glueing together different components in a
simple and easy way. Languages like bash, zsh were created to control shells
and allow calling multiple programs in a chain to achieve a goal. PHP and
JavaScript were created to control web features and make it more dynamic.
Python, Ruby, and Perl are more general purpose - with the goal of
facilitating rapid prototyping and expressiveness over computational speed.
Compilation and Interpretation
A complier translates the high-level source program into machine level
instructions which can directly be run on the computer.
An interpreter executes the high-level source program line by line or region
by region in a virtual machine.
In general, interpretation leads to more flexibility and dynamically inserting
code and the compiled version has better execution time.
When a program depends on the existence of a library, a linker is used to
link the library to the compiled version of a program.
Some compilers generate assembly rather than machine code to facilitate
debugging. Assembly code tends to be more human readable than machine code.
Compilers for C include a preprocessor step which removes comments and
expands macros. The preprocessor can able be instructed to remove portions of
the code itself based on the situation.
A lot of compilers are written in the languages that they compile. The Ada
compiler is written in Ada and the C compiler is written in C. This is done
using something called bootstrapping. One starts with a simple
implementation - often an interpreter - and uses it to build progressively more
sophisticated versions.
In some cases, a programming system may intentionally delay computation until
the last possible moment. Languages such as Prolog and Lisp that invoke the
compiler on the fly to translate newly created source code into machine
language.
"In a more general context, suppose we were building one of the first compilers
for a new programming language. Assuming we have a C compiler on our target
system, we might start by writing, in a simple subset of C, a compiler for an
equally simple subset of our new programming language. Once this compiler was
working, we could hand-translate the C code into (the subset of) our new
language, and then run the new source through the compiler itself. After that,
we could repeatedly extend the compiler to accept a larger subset of the new
programming language, bootstrap it again, and use the extended language to
implement an even larger subset. “Self-hosting” implementations of this sort are
actually quite common." (Taken directly from the book, 1.4).
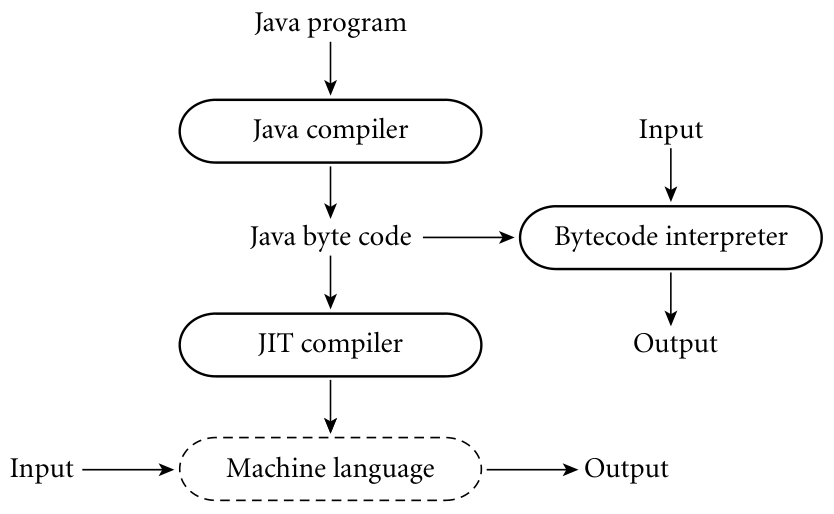
The Java definition defines a machine-independent form known as bytecode. The
first Java implementation were based on bytecode interpreters, the JVM (Java
Virtual Machine), but modern implementations obtain significantly better
performance with a just-in-time (JIT) compilation that translates bytecode
into machine code just before execution.
On some early machines (before 1980s), the assembly language instruction set is
not actually hardware, but in fact runs on an interpreter. The interpreter is
written in low-level instructions called microcode (or firmware), which is
stored in read-only memory and executed by hardware.
Overview of The Compilation Process
A typical compiler processes the input in a series of well-defined phases. Each
phase discovers information of use to later phases, or transforms the program
into a form that is more useful to the subsequent phase.
The first few phases serve to figure out the meaning of the source program. This
is sometimes called the front end of the compiler. The last few phases serve to
construct an equivalent target program. They are sometimes called back end of
the compiler.
An interpreter shares the compiler's front-end structure, but "executed"
(interprets) the intermediate form directly.
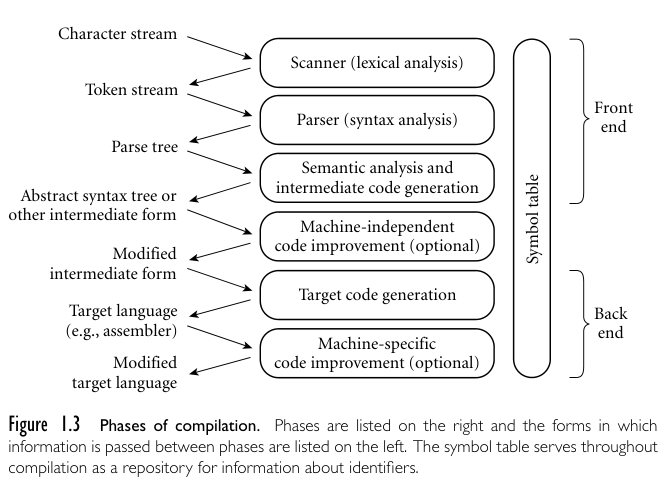
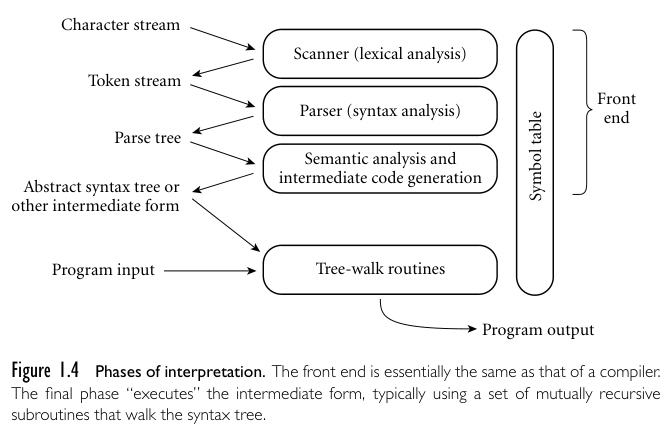
Lexical And Syntax Analysis
The first phase reads the characters of an input source code and groups them
into tokens such as int, main, {, etc. These are the smallest meaningful
units of the program. This scanning process is also known as lexical analysis.
The task of the scanner is to reduce the size of the input by converting
a sequence of characters to a sequence of tokens. It also typically removes
comments and tags tokens with line and column numbers, to make it easier to
generate good diagnostics in later phases.
Names, Scopes, And Bindings
Names
A name is a mnemonic character string used to represent something else.
Names act as a form of abstraction for memory addresses. When we code something
like value = 10, we actually just stored the value 10 at some memory
address.
The complete set of bindings of names in effect at a given point in a program is
known as the current referencing environment.
Bindings Time
A binding is mapping from a thing to its name. Binding time is the time at which
a binding is created or any implementation decision is made.
-
Language design time: Control-flow constructs, the set of primitive types,
the available constructors, etc are chosen when the language is designed.
-
Language implementation time: Most language manuals leave a variety of
issues to the discretion of the language implementer. This can be things such
as the precision of the fundamental types, the coupling of I/O to the
operating system's notion of files, etc.
-
Program writing time: Programmers choose algorithms, data structures, and
names.
-
Compile time: Compilers choose the mapping of high-level constructs to
machine code, including the layout of statically defined data in memory.
-
Link time: The linker chooses the overall layout of the modules, resolves
inter-module references, and finalizes the binding between objects in
different modules.
-
Load time: The operating system loads the program into memory, choosing
machine addresses for objects. Modern operating systems use virtual addresses
chosen at link time, while physical addresses can change at run time.
-
Run time: Covers the entire execution span, including variable bindings,
program start-up, module entry, elaboration time, subroutine call time, block
entry time, and expression evaluation/statement execution.
Object Lifetimes
The terms static and dynamic are generally used to refer to things bound
before run time and at run time, respectively.
Compilers tend to be more efficient at binding variables because they can make
earlier decisions. For example, a compiler analyzes the syntax and global
variables and arranges them for optimal access. It also can fix variable offsets
in the stack for function calls. Whereas the interpreter has to dynamically bind
global and local variables, sometimes for each time a function is called.
The time between the creation and the destruction of a name-to-object binding is
called the binding's lifetime. The time between creation and destruction of an
object is the object's lifetime.
-
Static objects are given an absolute address that is retained throughout the
program's execution.
-
Stack objects are allocated and deallocated in last-in, first-out order,
usually in conjunction with subroutine calls and returns.
-
Heap objects may be allocated and deallocated at arbitrary times. They
require a more general (and expensive) storage management algorithm.
Static Allocation
Global variables, the instructions that constitute a program's machine code,
numeric, and string values are examples of statically allocated objects.
Logically speaking, local variables are created when their subroutine is called,
and destroyed when it returns. If the subroutine is called repeatedly, each
invocation is said to create and destroy a separate instance of each local
variable.
However, this is not always the case and it is up to the language implementation
to create and destroy these local objects. Before Fortran 90 recursion was not
allowed since Fortran could only have one invocation of a function at any given
time.
Languages usually require named constants to have a value that can be determined
at compile time so that they can be statically allocated. Such constants and
literals are called manifest constants or compile-time constants. These
constants can always be static allocations, even if they are local to a
recursive subroutine.
Languages such as C and Ada have constants that are simply variables that cannot
be changed after elaboration (initialization) time. Their values, though
unchanging, can sometimes depends on other values that are not known until run
time. Such elaboration-time constants, when local to a recursive subroutine,
must be allocated on the stack. C# distinguishes between compile-time and
elaboration-time constants using the const and readonly keywords,
respectively.
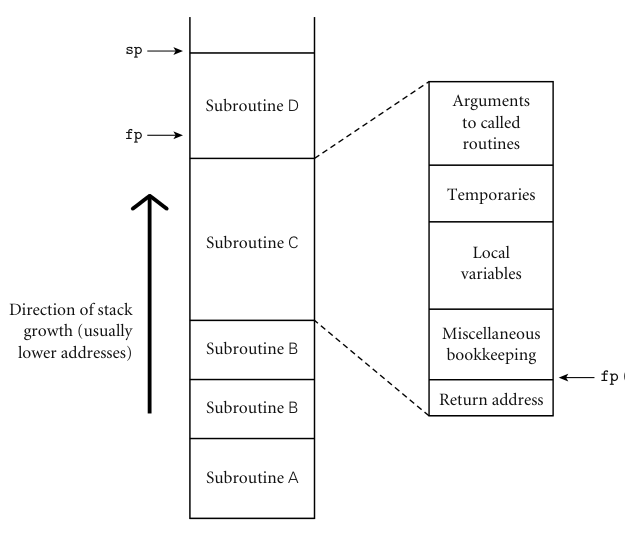
Stack-Based Allocation
If a language permits recursive, static allocation of local variables is no
longer an option, since the number of instances of a variable that may need to
exist at the same time is conceptually unbounded.
Each instance of the subroutine at run time has its own frame on the stack,
containing arguments, return values, local variables, temporaries, etc.
While the location of the stack frame cannot be predicted at compile time, the
offsets of objects within a frame usually can be statically determined.
Heap-Based Allocation
A heap is a region of storage in which sub-blocks can be allocated and
deallocated at arbitrary times. Heaps are required for the dynamically allocated
pieced of linked data structures, and for objects such as fully general
character strings, lists, and sets, whose size may change as a result of an
assignment statement or other update options.
The methods used for heap allocation is a balance between space and time
efficiency of the heap. Space concerns are further divided into internal and
external fragmentation of the heap. Internal fragmentation occurs when we
allocate more spaced than required to maintain a chunk size. External
fragmentation occurs when we allocate storage in a way such that the holes in
the memory are in such a way that new memory of a particular size cannot be
allocated.
For a more detailed explanation of internal and external fragmentation, read
notes from CSCI 3120 Operating
Systems.
There are multiple mechanisms to manage heap memory, these include:
- Linked list of free list
- Dynamic pool lists using buddy system ($2^k$)
- Dynamic pool list using Fibonacci heaps.
Garbage Collection
Heap allocation is trigged by some specific operation in a program such as
creating an object or calling malloc and so on. Deallocation is explicit in
some languages such as C, C++, and Rust but they can also be freed automatically
when the region is no longer reachable from the program. The latter method uses
something called a garbage collector which regularly checks and frees
unreachable objects.
The arguments in favor of explicit deallocation include implementation
simplicity and execution speed. Even naive implementation of garbage collection
add significant complexity to the implementation of the language.
However, manual deallocation errors are among the most common and costly bugs in
real-world programs. If an object is deallocated too soon, the program may
follow a dangling reference, accessing memory that may be used by another
object. If an object is not deallocated at the end of its lifetime, then the
program may leak memory, eventually running out of heap space. A garbage
collector solves these issues and reduces programming complexity and memory
management for programmers.
Rust has a unique solution to this problem where it does not have similar
memory deallocation issue even though it has explicit allocation and
deallocation. It uses a concept of ownership and borrowing to identify the
lifetime of an object.
Go/Golang is a complied language that has a garbage collector that is highly
optimized. Here is a comparison between go and rust:
source.
Scope
The textual region of the program in which a binding is active is its scope. In
most modern languages, the scope of a binding is determined statically at
compile time. This is purely set using simple textual rules and does not require
any run-time operations. C is statically scope, however, some languages may be
dynamically scoped were their bindings depend on the flow of execution at run
time.
At any given point in the program's execution, the set of active bindings is
called the current referencing environment.
Statically scoped variables are available globally. In C, the static keyword
creates a local variable that is allocated globally.
Interesting Fact: In C, the official specification requires that statically
declared variables are initialized to 0. This implies static int count would
create a variable count with the value 0.
void count_calls() {
static int count = 0;
count++;
printf("count_calls() called %d times.\n", count);
}
Nested Subroutines
The ability to nest subroutines inside each other, introduced in Algol 60, is a
feature of many languages such as Ada, ML, Common Lisp, Python, and a few
more. Other languages, including C and its descendants, allow classes or other
scopes to nest.
In the Algol-family of languages, the Algol-style nesting rules give rise to the
closest-nested scope rules where a name introduced in a declaration is only
known to the scope in which it is declared, and in each internally nested scope,
unless it is hidden by another declaration of the same name in one or more
nested scopes.
To find the object corresponding to a given use of a name, we look for a
declaration with that name in the current, innermost scope. If there is non, it
defines the active binding for the name. Otherwise, we look for a declaration in
the immediately surrounding scope. If no declaration is found at any level, then
the program is in error.
A name-to-object binding that is hidden by a nested declaration of the same name
is said to have a hole in its scope. Some languages provide qualifiers or
scope resolution operators to access names that have been rebound.
If a name is in the local scope then we can use a displacement from the base
register to find the variable. To find variable in different stack frames we
simple store a static link in each frame that points to the "parent" frame.
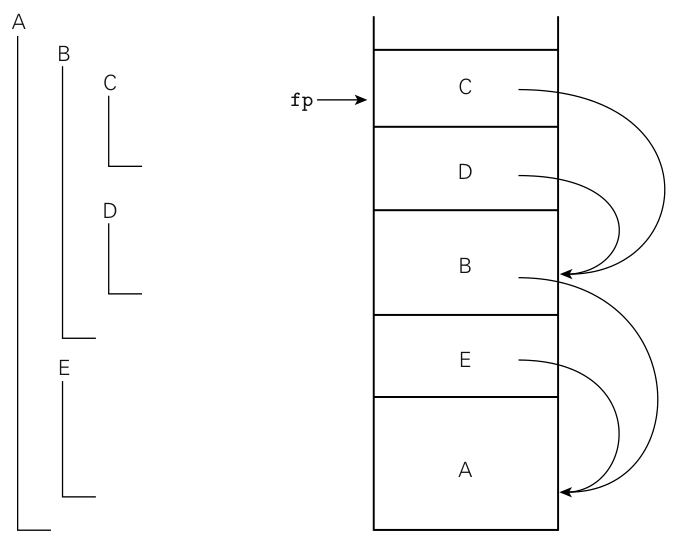
To find a variable or parameter declared in $j$ subroutine scopes outward,
target code at run time can dereference the static chain $j$ times and apply
the appropriate offset.
Declaration Order
Suppose an object $x$ is declared somewhere within block block $B$, can $x$ be
used in the section of $B$ before it has been declared? After all, $x$ is
defined inside of the scope of block $B$.
Several early languages required that variables be declared before they are
used. There are special mechanisms to accommodate recursive types and
subroutines, but in general, a forward reference (attempt to use name before
declaration) is a static semantic error.
But since a declaration is for the entire block, there are some interesting
errors that occur:
{
int X = 10;
{
int M = X;
int X = 20; // local declaration hides outer X
}
}
The above code in Pascal would lead to a semantic error since X is accessed
before it has been declared for that scope. The X that is used to initialize
M is the X within the inner scope.
In Ada, C, C++, or Java, no semantic errors would be reported. The declaration
of $M$ would refer to the first (outer) declaration of $X$. The scope of a
variable is not whole-block but rather from the point of declaration till the
end of the block.
JavaScript uses a concept called hoisting so that variables can be declared in
any part of the block are moved to the top of the block. This way, something
like this is valid in JavaScript:
x = 5; // Assign 5 to x
elem = document.getElementById("demo"); // Find an element
elem.innerHTML = x; // Display x in the element
var x; // Declare x
Declarations And Definitions
Recursive types and subroutines introduce a problem for languages that require
names to be declared before they can be used. C and C++ handle the problem by
distinguishing between the declaration of an object and its definition.
A declaration introduces a name and indicates its scope, but may omit certain
implementation details. A definition describes the object in sufficient detail
for the compiler to determine its implementation.
Examples:
struct manager; // declaration
struct employee {
struct manager *boss;
struct employee *next_employee;
};
struct manager { // definition
struct employee *first_employee;
};
And for a function definition:
void list_tail(follow_set fs); // declaration only
void list(follow_set fs) {
switch (input_token) {
case id: match(id); list_tail(fs);
// ...
}
}
void list_tail(follow_set fs) { // definition
switch (input_token) {
case comma: match(comma); list(fs);
}
}
The initial declaration of manager only needs to introduce a name since
pointers are generally the same size. The compiler can determine the
implementation of employee without knowing any details about manager. On the
other hand, the initial declaration of list_tail must include the return type
and the parameter list. This way, the compiler can verify that the call in
list is correct.
Predefined Objects
Declared in an outermost scope that is outside the program's global scope. This
can include things like addition, multiplication, etc. This permits the
redefinition of such names.
Dynamic Scope
The binding for a given name depends on the order of execution - it's the most
recently encountered during execution but not yet destroyed by exiting its
scope.
n : integer
procedure first()
n := 1
procedure second()
n : integer
first()
n := 2
if read_integer() > 0
second()
else
first()
In the above code snippet the n inside of the first procedure refers to the
global n in the else block and refers to the n defined in the second
procedure in the if true block. This is because, n was redefined by the
second procedure.
Modules
A way to group multiple names together. Breaking down larger projects into
modules makes it easier to reason about code.
Modules enable information hiding:
- Modules provide simple interfaces
- Reduce risk of naming conflicts
- Reduce coupling
- Reduce cognitive load
- Increase code re-use.
In C, you cannot share static variables among multiple subroutines.
C++ introduces namespaces to help solve similar problems.
#include <time.h>
namespace rand_mod {
unsigned int seed = time(0);
const unsigned int a = 48271;
const unsigned int m = 0x7fffff;
void set_seed(unsigned int s) {
seed = s;
}
unsigned int rand_int() {
return seed = (a * seed) % m;
}
}
Imports and Exports
Modules use imports and exports to expose and include modules features. Exports
restrict the names that a module exposes, and possibly the manner in which those
names can be used in a client module. Imports identify the names exported by an
external module that a client module wishes to include in its scope.
Modules into which names must be explicitly imported are called closed
scopes.
Modules which do not require imports are called open scopes.
Object-Oriented Extension
Object-oriented programming is a natural extension of modules, they allow us to
encapsulate data and methods. They have the advantage of remembering state on a
per-object basis.
Referencing Environments
-
Static scoping: The referencing environment depends on the lexical nesting of
the code blocks where names are declared. This can be determined at compile
time.
-
Dynamic scoping: The referencing environment depends on the order in which
declarations are encountered at run time.
Deep vs Shallow Binding
A deep binding refers to the referencing environment that exists when some
function f was passed applies to f. (The moment f was created).
A shallow binding refers to the referencing environment when f is invoked
applies to f. (The moment f was called).
Deep binding is implemented by creating a representation of the referencing
environment and bundling it with a reference to the subroutine. This bundle is
referred to as a closure.
Unlimited Extent
Subroutines in a functional language have first-class status. They can be
passed as a parameter, returned from a subroutine, assigned to a variable, etc.
A reference to a subroutine may outlive the scope which the subroutine is
declared.
; Function takes a param x and returns a function
; such that f(y) return x+y
(define plus-x
(lambda (x)
(lambda (y)
(+ x y)
)
)
)
(let ((f (plus-x 2)))
(f 3)
) ; return 5
The 2 was on the stack as a parameter and then has been popped off the stack.
But f remembers 2 even though x is no longer on the stack. The local
variable x has unlimited extent. It may not be garbage collected until no
references to the value of plus-x 2 remain.
Object Closures
-
Global (top-level) functions, when passed, use the global referencing
environment.
-
Nested functions, on the other hand, require non-trivial referencing
environments.
By encapsulating a function in an object, we can include the function's
context in that object.
Lambda Expressions
A lambda expression is an anonymous function.
- Scheme:
(lambda (i j ) (if (> i j) i j))
- C#:
(int i, int j) => i > j ? i : j
- OCaml:
fun i j -> if i > j then i else j
- Ruby:
-> (i, j) { i > j ? i : j}
C++ adopted lambda expression in C++ 11. However, lacking a garbage collector,
the notion of unlimited extent is unworkable.
Suppose we want a lambda expression to print values less than some variable k.
There are two options:
By value:
[=](int e){ if (e < k) cout << e << " "; }
In this case, the lambda expression is evaluated at runtime and k is just
stored as a value inside of the lambda expression. Copying a large data
structure can be expensive. External updates to those variables will not be
reflected in future calls to the closure. But this allows closures to be used
even when copied variables leave scope.
Or by reference:
[&](int e){ if (e < k) cout << e << " "; }
This can lead to undefined behaviour if the referenced variable leaves scope.
External updates to references variables will be reflected in future calls.
References are just pointers and are less expensive to copy.
Control Flow
Constructs
-
Sequencing: instructions should be executed in a specified order.
-
Selection: at run-time, some choices between alternative execution paths need
to be made.
-
Iteration: some sequence of instructions needs to be executed repeatedly,
either a pre-determined number of times, or until some condition is true or
false.
-
Subroutines: Encapsulate a potentially complex sequence of instructions so
that it can be treated as a unit.
-
Recursion: An expression that is defined in terms of itself. Usually
implemented as one or more self-referential subroutines.
-
Concurrency: Two or more parts of a program are to be executed simultaneously.
-
Exception Handling: Handling unexpected run-time conditions.
-
Non-determinism: Ordering among instructions is deliberately unspecified.
Expressions
Literals, named variables, named constants, operators or functions applied to
one or more arguments.
-
A prefix expression: -x, Math.sin(Math.PI), (+ 1 2)
-
A infix expression: a + b
-
A postfix expression: a b + or PI sin
Lisp and Scheme use prefix Cambridge Polish notation exclusively (prefix
expressions).
Forth uses postfix notation and special stack handling; Simple expressions are
pushed onto the stack and functions and operators pop their arguments off the
stack, and push their return values on.
Infix notation leads to potential ambiguity: a + b * c could either be (a +
b) * c or a + (b * c). This is solved by operator precedence. Sequence of
equal-precedence operators group to the left or the right (associativity).
Value Model
Languages like C employ a value model of variables. Variables are treated as
containers for values. Locations appear on the left side of the assignment
operator, and values on the right. Thus referred to as l-values and r-values
respectively.
Consider: f(a)[2] = 12;
Here the function returns a pointer and we're setting the index 2 to the value
12.
Reference Model
Languages like Clu employ a reference model where variables are not container
for values but a named reference to the value.
In languages where values can change in-place, the difference between the value
model and the reference model play a strong role.
Example:
class A:
def __init__(self):
self.m = 10
a = A()
b = a
a.m = 20
print(b.m) # 20
Update Operations
Consider the following situation:
A[index_fn(i)] = A[index_fn(i)] + 1;
If index_fn has a side-effect, multiple calls may return multiple values.
Therefore, something like this makes it more clear:
Prefix operations perform the operation first where as postfix first evaluates
the variable and then increments it.
int x = 5;
int y, z;
y = x++; // y = 5, x = 6
z = ++x; // z = 7, x = 7
The evaluation order where side effects are presents may be problematic:
fib[++i] = fib[i] + fib[i-1]
Depending on which side is evaluated first is going to change the operation that
is performed in the above snippet. Evaluation order can be situation dependent.
A compiler may choose evaluation order to take advantage of certain registers or
instructions, in an effort to improve performance.
Such statements are classified as undefined behaviour in C. This includes
statements where there are multiple increment or decrement operators such as:
Initialization
Accidental use of an uninitialized variable is a very common programming error.
-
An easy way to prevent such errors is to ensure that every variable receives a
value when it is first declared.
-
Some languages initialize variables to zero by default.
-
Others use dynamic checks to establish that variables are assigned values
before they are used.
-
Languages like Java and C# define a notion of definite assignment, where the
compiler establishes that every path between declaration and use assigns a
value to the variable.
Unstructured Programming
Older imperative languages like Fortran and Basic used labels to identify
statements. Branching and looping used GOTO label and GOSUB label to direct
program flow.
10 X = X + 1
20 PRINT X
30 GOTO 10
This is a holdover from machine and assembly language. goto is still a part of
C. It is very easy to accidentally create an infinite loop using goto. Java
reserves goto as a keyword, but does not permit its use.
Structured Programming
In structured programming languages like Algol, and virtually every programming
language since, goto is replaced by constructs such as if-else and switch-case
for selection and for, while, do-while, repeat-until for iteration.
Recursion
Every iterative procedure can be replaced with recursion:
while (cond) {
// statements
}
// same as
void p() {
if (cond) {
// statements
p()
}
}
The converse however, is not true. Not every recursive can be made iterative in
a "simple" way - without using additional data structures.
The recursive example can be translated by the compiler back into a loop; using
a technique called tail-recursion elimination.
Exception
An exception is an unexpected or unusual condition that occurs during execution
that cannot be easily handled locally.
Some ways to handle exceptions:
- Return a special value, eg: -1 for find indexed function.
- Return an explicit status value to the caller, through an extra argument or a
return tuple.
- Caller passes an error handling closure to the callee.
Example of return special value as error (C):
int find_element(int element, int length, int *array) {
for (int i=0; i<length; i++) {
if (array[i] == element) {
return i;
}
}
return -1
}
int main() {
int a[] = {1, 2, 3};
if (find_element(4, 3, a) == -1) {
// element not found
}
}
An example of an explicit status return (Go):
func findElement(element int, array []int) (int, error) {
for i, value := range array {
if value == element {
return i, nil
}
}
return -1, errors.New("element not found")
}
func main() {
a := []int{1, 2, 3}
if _, err := findElement(4, a); err != nil {
// element not found
}
}
Exception Handling
Originally appeared in PL/I where we have the following structure:
The nested statement isn't executed immediately, instead it is remembered and
only invoked when the exceptional condition is encountered. Dynamic binding of
exceptions to handles is confusing and error prone.
To handle requirement of a particular exception in different ways based on the
situation the exception occurs in, we have lexically bound exception
handlers:
try {
if (something_unexpcted) {
throw my_error("oops!");
}
} catch (my_error e) {
// handle exception
}
Here the exception handler is lexically bound to the try block, as opposed to
dynamically bound at runtime as in PL/I.
Exceptions have types, and those types may include one or more fields to contain
debugging information and messaging. If no matching handler is bound to the
current try block, the exception is raised again to the current subroutine's
caller. The exception propagates up the call stack until a matching handler is
found, or we reach the top of the stack (which normally terminates the program).
To handle exceptions, we may need to unwind any stack frames belonging to
subroutines from which the exception escapes. Other resources may also need to
be released. Here the finally block is executed regardless of whether the
try block completes normally, or terminates prematurely as the result of an
exception.
try:
my_stream = open("foo.txt", "r")
for line in my_stream:
# Other code
finally:
my_stream.close()
Type Systems
-
A denotational view of types is where a type is a set of values, or domain.
-
A structural notion is where a type is either primitive, or composite such as
classes, structs, arrays.
-
An abstract notion of type is where a type is an interface consisting of a set
of operations with well-defined and mutually consistent semantics.
Structures
A structure or struct is a collection of named fields with types.
struct element_t {
char symbol[3];
int atomic_number;
double melting_point;
bool is_metal;
}
The memory layout of the struct may be stored in different ways based on the
language.
Memory Layout
Aligned
struct element_t {
char symbol[3];
int atomic_number;
double melting_point;
bool is_metal;
}
The aligned or fixed order way to organize the struct in memory would be to
arrange them in the order of declaration while aligning them to a particular
memory boundary.
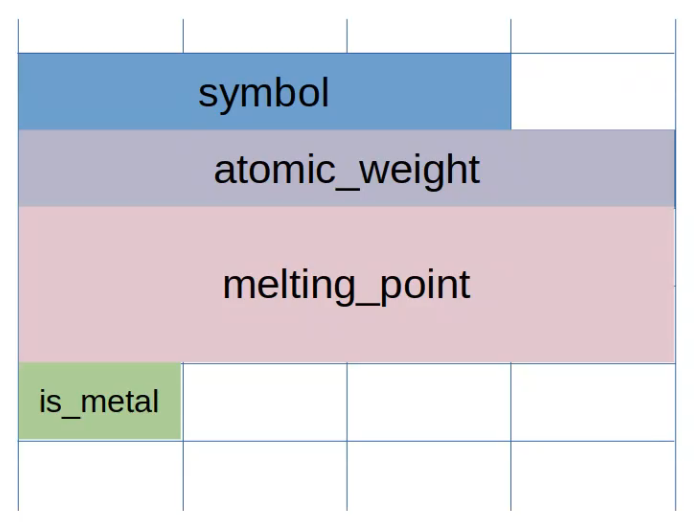
This kind of alignment is done to optimize memory access since most computer
access more than one byte in one read operation.
Therefore, in the particular case above, our struct takes up 24 bytes even
though our struct only requires 16 bytes (in C on a 64 bit machine).
Here is the code that was used to test this:
#include <stdio.h>
#include <stdbool.h>
struct element_t {
char symbol[3];
int atomic_number;
double melting_point;
bool is_metal;
};
int main() {
size_t sum_size = sizeof(char [3]) + sizeof(int) + sizeof(double) + sizeof(bool);
size_t real_size = sizeof(struct element_t);
printf("sum of size of element: %ld\n", sum_size);
printf("size of struct: %ld\n", real_size);
}
This leads to faster memory access and preserves the order in which elements are
declared but lead to inefficient use of space. This also guarantees the order of
the memory layout so if manual memory manipulations are performed then the order
is predictable.
We can manually re-order the elements to minimize the wasted space. C aligns
elements in multiples of the largest previous element.
So if we use something like this, where the elements are arranged in increasing
order of size used, we can get a more optimized layout:
struct element_t {
bool is_metal;
char symbol[3];
int atomic_number;
double melting_point;
};
Our struct now only takes up 16 bytes of space and all those 16 bytes are
used for the struct.
Packed
In the packed method of organizing memory, we optimize for space while still
preserving the order of the struct.
struct element_t {
char symbol[3];
int atomic_number;
double melting_point;
bool is_metal;
}
The above struct would then be arranged as follows:
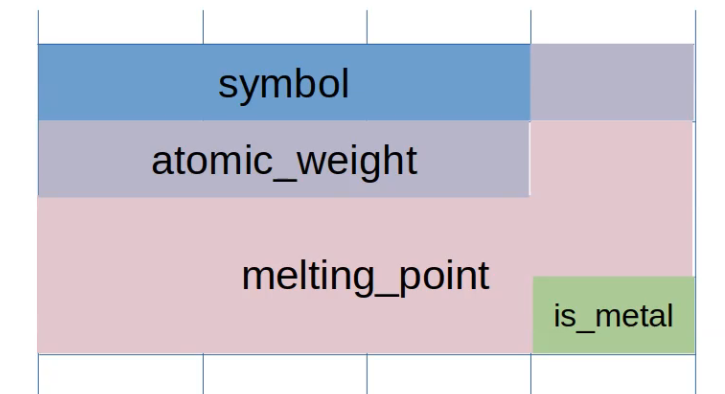
But this causes element access to be much slower since a lot of operations have
to be performed to read a single element if it is not aligned right. This still
guarantees the memory layout.
Optimized Aligned
The compiler optimizes the struct to minimize space while still maintaining the
alignment of the elements. This way, the space and speed are optimized. However,
this may cause the struct to be reordered, hence leading to a non-guaranteed
memory layout.
struct element_t {
char symbol[3];
int atomic_number;
double melting_point;
bool is_metal;
}
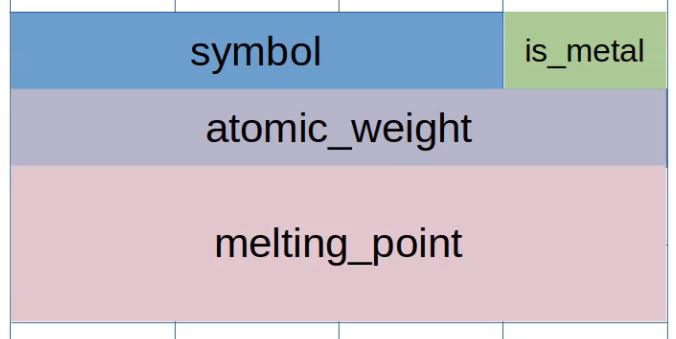
Rust is a language that employs this technique and hence specifies that the
memory layout is undefined.
This also leads memory layout may be compiler or architecture dependent.
Arrays
Collections of objects of a single type (typically) occupying a contiguous
region of memory.
- Static Arrays: Type and shape are known at compile time.
- Heap Arrays: Type and dimensionality may be known at compile time and shape
known at run time.
Dead Reckoning
For a one-dimensional array at memory location A whose elements are of type T,
we can calculate the address of an element at index n using the following
calculation:
Where A is the base address of the array and sizeof(T) is the array's
stride, or the width of each element.
Dope Vectors
A dope vector stores metadata about the memory layout of a data object (like an
array). This would include the base address, stride and the sizes of each
dimension.
This way the array can then grow if necessary by replacing the metadata in the
dope vector.
Scheme
Scheme is a function programming language. Almost everything in scheme is a
function. Functional languages are mostly pure, in the sense that they avoid
side-effects and updating variables.
Development Environment
We can use DrRacket as an environment to run scheme. We begin files with a
#lang directive that identifies the programming language a file is written in.
We start the file with #lang scheme to indicate the language scheme.
DrRacket Website
Hello World
Here's how you'd write a hello world program in scheme.
#lang scheme
(display "Hello, World!")
Note that #lang scheme is required if we're using a racket interpreter.
For something more complex, here is a implementation of the Fibonacci sequence:
#lang scheme
(define (fibonacci n)
(if (<= n 2)
1
(+ (fibonacci (- n 1)) (fibonacci (- n 2)))
)
)
(define (displayFibonacciTill n)
(if (<= n 0)
0
(begin
(displayFibonacciTill (- n 1))
(display
(string-append
(number->string n)
" "
(number->string (fibonacci n))
"\n")
)
)
)
)
(displayFibonacciTill 40)
Language Features
Identifiers
These identifiers include keywords, variable, and symbols. These maybe formed
from letters, numbers, and certain special characters:
Identifiers cannot start with the @ symbol and normally cannot start with any
character that can start a number, i.e., a digit, decimal point (.).
Exceptions are +, -, and ..., which are valid identifiers.
Valid identifiers include: hi, Hello, n, x, x3, x+2, ?$&*!!!.
Atomic Values
The following are all atomic values:
- Boolean values such as
#t and #f
- Numbers:
- Integers:
-2, -1, 0, 1, 2
- Real:
0.5, 1.333, 97.423, pi
- Rationals:
1/2, 4/3, 9/10, 22/7
- Complex:
3+4i
- Strings:
"Hello World!"
Cells or Pairs
Cells or pairs are a structured data type consisting of two parts named car,
and cdr. For example, '(1 . 2) is a pair literal with car of 1 and cdr
of 2.
The leading single quote indicates a pair literal (as opposed to an expression).
Cells can be combined to produce lists.
Proper and Improper Lists
Cells can be combined to produce lists. '(a b c) is a pair literal with car
a and cdr '(b c).
- The value of
'() is known as a nil or null is the empty list.
- The value
'(a) is a pair literal with car a and cdr '().
A proper list is either the empty list '() or a pair whose cdr is a proper
list. Any other pair is an improper list.
'(), '(a), and '(a b c) are all proper lists.'(1 . 2) is not since its cdr, 2, is not a proper list.
Note that '(1 . 2) is not the same as '(1 2). The first is an improper list
while the second is a proper list.
Non-literal Expressions
All non-literal expressions in Scheme have the same overall form:
Where:
operator is an operator or function identifiera1 a2 ... an are the operands/arguments to that operator or function- Arguments can be literals or non-literal expressions themselves.
The above statement would be the same as the following C-like statement:
operator(a1, a2, ..., an)
Boolean Operators
not, and, and or are the boolean operations. Note that all expressions in
scheme that is not explicitly #f is treated as #t. That is, 0 has a
"truthy" value of #t, 1 has a value of #t, etc. Only the #f has the
value of false.
-
(not a) returns #t if its argument a is #f, it returns #f otherwise.
-
(and a1 a2 ... an) returns an if all its arguments a1 ... an-1 are not
false, #f otherwise.
-
(or a1 a2 ... an) returns the first ai that is not false. Or #f iff all
ai are false.
Note that both and or or exhibit short-circuit evaluation. Only as many ai
will be evaluated as necessary.
Arithmetic Operators
(- a) returns the negation of its argument a.(- a1 a2 a3 ... an) returns a1 - a2 - a3 - ... - an.(/ a) returns the reciprocal of its argument a.(/ a1 a2 ... an) returns a1 / a2 / a3 / ... / an.- Addition
+ and multiplication * work the obvious way.
Numeric Comparison Operators
-
(= a1 a2 ... an) returns #t if a1 = a2 = ... = an
- otherwise
#f
(= 1 1+0i 3/3) is #t
-
(< a1 a2 ... an) returns #t if a1 < a2 < ... < an
- otherwise
#f
(< 1 2 2.5 pi 16/4) is #t
-
(> ...), (>= ...), (<= ...) work similarly.
Basic Numeric Predicates
Predicates are functions that return a boolean value.
(number? a) returns #t iff a is a number.(natural? a) returns #t iff a is a natural number.(integer? a) returns #t iff a is an integer.(rational? a) returns #t iff a is a rational number.(real? a) returns #t iff a is a real number.(complex? a) returns #t iff a is a complex number.(exact? a) returns #t iff a is an exact value.(inexact? a) returns #t iff a is an inexact value.
Basic Pair Functions
These are functions that work on pairs or lists.
(car a) returns the car of a(cdr a) returns the cdr of a(cons ar dr) returns the pair '(ar . dr)(list a1 a2 .. an) returns the proper list '(a1 a2 .. an)(list? a) returns #t iff a is a proper list(null? a) returns #t iff a is the empty list '()
Conditionals
If Else
(if condition if-true if-false)
This evaluates the given condition and returns if-true if the condition
evaluates to anything but #f. It returns if-false if the condition evaluates
to #f.
Example:
(display
(if (= n 1)
2
4
)
)
This if-statement returns 2 if n is equal to 1 and returns 4 otherwise.
Switch/Cond
(cond (condition_1 return_1) (condition_2 return_2))
This evaluates each condition_i in turn. When a condition_i evaluates to
#t the corresponding return_i value is returned. Conditions after the
succeeding one are not evaluated. Only the corresponding return value is
evaluated. Returns nothing if no condition evaluates to #t. Can use #t as a
condition to implement a default.
Example:
(display (cond
((= n 1) 2)
((= n 2) 4)
(#t 0)
))
;; Or similarly
(display (cond
((= n 1) 2)
((= n 2) 4)
(else 0)
))
The above cond statement returns 1 if n=1 and 4 if n=2. If neither of
those evaluates to #t, the last statement is run and the statement returns
0.
Racket returns #<void> if no condition is matched.
Local Binding With Let
(let ((name1 expr1) (name2 expr2) ...) expression)
This evaluates expression with the given names bound to the corresponding
expressions. Note that these variables must be independent of each other.
expr2 cannot reference name1.
There is also let* which is the same as let except that variables may
reference predecessors.
Lambda Expressions
(lambda (name1 name2 .. namen) expression)
Evaluates to an anonymous function which returns the value of expression when
argument names name1, name2, ..., namen are bound to corresponding
argument values.
Examples:
The above creates an anonymous function with one argument named x which
returns the value of x plus two.
Global Binding with Define
This creates a global binding of the given name to the given value.
Here are some examples:
(define e 2.7182818)
; generally define used to create new functions
(define plus-2 (lambda (x) (+ x 2)))
; there is a shorthand for convenience
(define (plus-2 x) (+ x 2))
Unit Testing
We use a library called rackunit: https://docs.racket-lang.org/rackunit/.
(require rackunit)
; Check if expression equals to #t
(check-true expression)
; Check if expression evaluates to #f
(check-false expression)
; Check if expression does not evaluate to #f
(cehck-not-false expression)
; Verifies that (equal? actual expected) evaluates to #t
(check-equal? actual expected)
Recursion
Iteration structures like for or while are problematic in functional
languages like Scheme since they involve updating loop variables.
All loops can be replaced with recursion.
void func(n) {
for (int i = 0; i<n; i++) {
// do something
}
}
The above can be converted to something like this:
(define (func n) (
(if (> n 1)
(begin
; do something
(func (- n 1))
)
)
))
This is called tail-recursion which is when the function calls itself as the
very last thing the function does.
Challenge With Recursion
Here is an example of the factorial function in scheme:
(define (factorial n) (
(if (< n 2)
1
(* n (factorial (- n 1)))
)
))
This is a fairly typical definition of the factorial function. But it isn't
tail-recursion since the multiplication step can only occur after the recursive
call. The challenge here is that for even moderate values of $n$, we will
overflow the stack (each recursive call is going to create a new stack frame).
Tail-recursion is handle uniquely in that it doesn't create a new stack frame
but rather replaces the stack frame with the new stack frame, at least in
DrRacket.
Named Let
A named let in Scheme is a let expression that behaves like a local function
definition.
The main advantage of a named let is that it creates a function that can be
called recursively from inside the expression.
(let name ((var1 value1) (var2 value2) ...)
expression
)
When a named let is first encountered, it behaves like a normal let but it
also defines the local function (define (name var1 var2 ...) expression) and
this function can be called recursively from inside expression.
We used named let to define a local function fact that takes two arguments:
m which identifies which factorial we are on, and p its factorial. This way
of defining the function allows us to use tail-recursion.
(define (factorial n)
(let fact ((m 0) (p 1))
(if (= n m)
p
(fact (+ m 1) (* p (+ m 1)))
)
)
)
List Patterns
In imperative programming languages we use some common list transformation
patterns on lists. There are three common functions that are commonly used.
map: The function applies a function to every element of a list.filter: The function builds a sub-list containing elements that satisfy a
predicate.reduce: Accumulates the elements in a list into a single result based on an
operation.
map and filter are built-in functions in scheme. reduce can be imported
from the library srfi/1 using the expression (require srfi/1).
Here is an implementation of the functions with an example of the use-case:
(define (map func lst)
(if (null? lst)
'()
(cons (func (car lst)) (map func (cdr lst)))))
(define (filter pred lst)
(cond ((null? lst) '())
((pred (car lst)) (cons (car lst) (filter pred (cdr lst))))
(else (filter pred (cdr lst)))))
(define (reduce func init lst)
(if (null? lst)
init
(reduce func (func init (car lst)) (cdr lst))))
(define (even? x)
(= (remainder x 2) 0))
(define (square x)
(* x x))
;; Function to sum the squares of all even numbers
(define (square-sum-evens numbers)
(reduce +
0
(map square
(filter even? numbers))))
;; Example usage
(square-sum-evens '(1 2 3 4 5 6))
Apply
The apply function allows us to apply a function to a list of arguments.
Zip
Sometimes we have two or more lists where the $i^{th}$ element of each list
corresponds with one another. The zip function accepts $n$ lists of length $l$
and return $l$ lists of length $n$ comprised of $i^{th}$ element of each
incoming list.
Like reduce, the zip function is part of the srfi/1 library.
;; Helper function to add elements of a pair
(define (sum-pair pair)
(apply + pair))
;; Using zip and map to add corresponding elements of two lists
(define (sum-pairs list1 list2)
(map sum-pair (zip list1 list2)))
;; Example usage
(sum-pairs '(1 2 3) '(4 5 6)) ; Expected output: '(5 7 9)
Examples Of Scheme
This repository contains examples of Scheme and Prolog code examples:
GitHub Repository.
The following are some examples from that repository.
Lukas Numbers
#lang scheme
(define (lukas n)
(cond ((= n 0) 2)
((= n 1) 1)
(#t (let next-iteration ((m 2) (lnum1 (lukas 0)) (lnum2 (lukas 1)))
(let ((lm (+ lnum1 lnum2)))
(if (= n m)
lm
(next-iteration (+ m 1) lnum2 lm)
)
)
))
)
)
(display (lukas 30))
Sequence Generators
#lang scheme
; Calculate the next term in the sequence given the
; current terms and the coefficients.
; next = term[0] * coefficients[0] + term[1] * coefficients[1] ...
; Assumes length of terms and coeffs are the same.
(define (calculate-next-term terms coeffs)
(if (equal? terms '())
0
(+
(* (car terms) (car coeffs))
(calculate-next-term (cdr terms) (cdr coeffs))
)
)
)
; Get a function to generate terms of a linear recurrence relation
; defined on a set of initial terms and coefficients.
; Assumptions:
; - initial-terms and coefficients match in length
; - the sequence starts from 0. i.e.,
; the last element of initial-terms is the 0th term.
(define (sequence-generator initial-terms coefficients)
(lambda (n)
(let ((len_terms (length initial-terms)))
(if (< n len_terms)
(list-ref initial-terms n)
(let function ((index len_terms) (terms initial-terms))
(let ((next-term (calculate-next-term terms coefficients)))
(if (= n index)
next-term
(function (+ index 1) (append (cdr terms) (list next-term)))
)
)
)
)
)
)
)
; A function to get the nth term in the padovan series
; padovan(0) = 0; padovan(3) = 2; padovan(10) = 12
(define padovan (sequence-generator '(1 1 1) '(1 1 0)))
(require rackunit)
; Fibonacci Sequence Test
(define fibonacci_test (sequence-generator '(0 1) '(1 1)))
(check-equal? (fibonacci_test 0) 0)
(check-equal? (fibonacci_test 1) 1)
(check-equal? (fibonacci_test 5) 5)
(check-equal? (fibonacci_test 10) 55)
; Padovan Sequence Test
(define padovan_test (sequence-generator '(1 1 1) '(1 1 0)))
(check-equal? (padovan_test 0) 1)
(check-equal? (padovan_test 1) 1)
(check-equal? (padovan_test 2) 1)
(check-equal? (padovan_test 3) 2)
(check-equal? (padovan_test 4) 2)
(check-equal? (padovan_test 5) 3)
(check-equal? (padovan_test 6) 4)
(check-equal? (padovan_test 10) 12)
(define pad1000 95947899754891883718198635265406591795729388343961013326205746660648433358757497113284765865744376976832226705511219598880)
(check-equal? (padovan_test 25) 816)
(check-equal? (padovan_test 40) 55405)
(check-equal? (padovan_test 100) 1177482265857)
(check-equal? (padovan_test 1000) pad1000)
; Lucas Numbers Test
(define lucas_test (sequence-generator '(2 1) '(1 1)))
(check-equal? (lucas_test 0) 2)
(check-equal? (lucas_test 1) 1)
(check-equal? (lucas_test 2) 3)
(check-equal? (lucas_test 3) 4)
(check-equal? (lucas_test 4) 7)
(check-equal? (lucas_test 4) 7)
(check-equal? (lucas_test 39) 141422324)
Prolog
Prolog is a logic programming language. Such as language uses facts and rules to
determine the results of queries.
Swish Online Interpreter
Atoms
The fundamental pieces of Prolog are atoms. Atoms are mere tokens and represent
whatever the programmer intends. They are constructed using:
- String of letters, digits, underscores starting with a lowecase letter.
- Strings of special characters. (Some strings of special characters have predefined meanings)
- Strings of characters enclosed in single quotes.
The atom socrates only has meaning because the programmer has decided that it
does. It could refer to the Greek philosopher or a cat.
Compound Terms
A compound term consists of a name (an atom) and one or more arguments (which
are arbitrary Prolog objects).
Query Resolution
Query are resolved by Prolog using backtracking. It uses a depth-first search
from the top to the bottom to find facts and rules that can be unified with the
current goal.
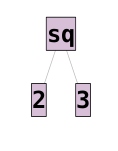
Terms
Prolog treats terms like sq(2, 3) as a tree:
It even treats expressions as trees 2 * 4 + 7:

The principle functor of a term is the name and arity of the root node in
the term's tree representation.
The principle functor of sq(2, 3) is sq/2 and the principle functor of 2 *
4 + 7 is +/2.
Precedence And Associativity
Each operator has a precedence between 1 and 1200 and an associativity:
- For prefix operators
fx or fy.
- For infix operators
xfx, xfy, yfx, or yfy
- For postfix operators:
xf or yf
In all cases f represents the operator x and y follow the following rules:
x represents an argument that must have STRICTLY lower precedence.y represents an argument that must have lower or equal precedence.
| Precedence |
Associativity |
Symbol |
| 1200 |
xfx |
:- |
| 1200 |
fx |
:- ? |
| 1100 |
xfy |
; |
| 1000 |
xfy |
, |
| 700 |
xfx |
list below |
| 500 |
yfx |
+ - |
| 500 |
fx |
+ - |
| 400 |
yfx |
* / // |
| 200 |
xfx |
** |
| 200 |
xfy |
^ |
List for 700 xfx: = =:= < =< == =\= > >= \= is.
For the expression: 2 * 4 + 7:
The atoms 2, 4, and 7 all have precedence 0. The * operator has
precedence 400 and the + operator has precedence 500.
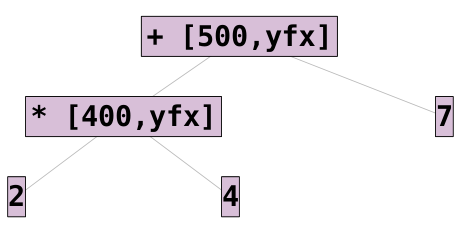
The * cannot be the principle functor since the child node must have lower
precedence. This has one exception with regards to parenthesis: ().
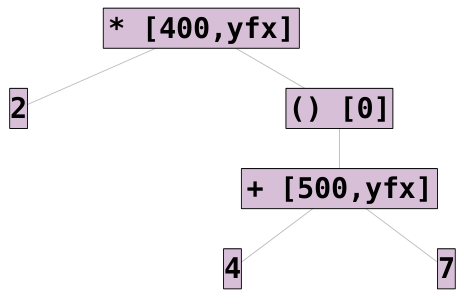
2 * (4 + 7): To achieve this interpretation, we would need to wrap part of the
expression in parenthesis. This reduces the precedence of the parenthesized
expression to zero.
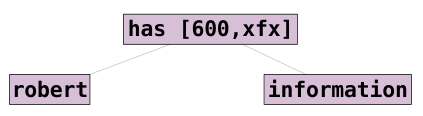
Custom Operators
Prolog permits the declaration of custom operators:
?- op(600, xfx, has).
robert has information
The above statement is equivalent to has(robert, information).